AI Mathematical Proof: Which Came First, the Chicken or the Egg?
Introduction
[Part 2: Proof: This covers Perplexity AI’s mathematical proof.]
I set out to apply AI to resolve a long-standing theory I have had regarding the “chicken or the egg” problem.
I realized that I could entice AI to develop a mathematical proof to confirm or quash my theory.
I utilized Perplexity’s Deep Research model to develop the proof. I then fed Perplexity’s mathematical proof into Google Gemini 2.5 to verify it.

This is our breakdown of the problem:
- Introduction
- My Theory
- AI: Theory Analysis
- AI: Mathematical Proof [this page]
- AI: Validation of Proof


AI: Mathematical Proof

Proof Summary: Why the Egg Came First
-
Genetic definition: A “chicken egg” is defined by containing an embryo with chicken DNA, not by the species of its parent.
-
Mutation timing: The first true chicken arose from a genetic mutation within an egg laid by a near-chicken (“proto-chicken”).
-
Temporal priority: The egg with the mutated chicken DNA existed before the chicken inside it hatched.
-
Parent paradox: The organism that laid this egg was not a chicken, avoiding infinite regress.
-
Formal logic: If C = first chicken, then C hatched from egg E. By definition, E is a chicken egg and predates C.
-
Alternative rejected: Defining eggs by parental species (vs. genetics) reverses the conclusion but misrepresents evolutionary biology.
Conclusion: Under evolutionary principles, the egg containing the first chicken genetically preceded the chicken itself. 🥚→🐔
response: Perplexity Deep Research
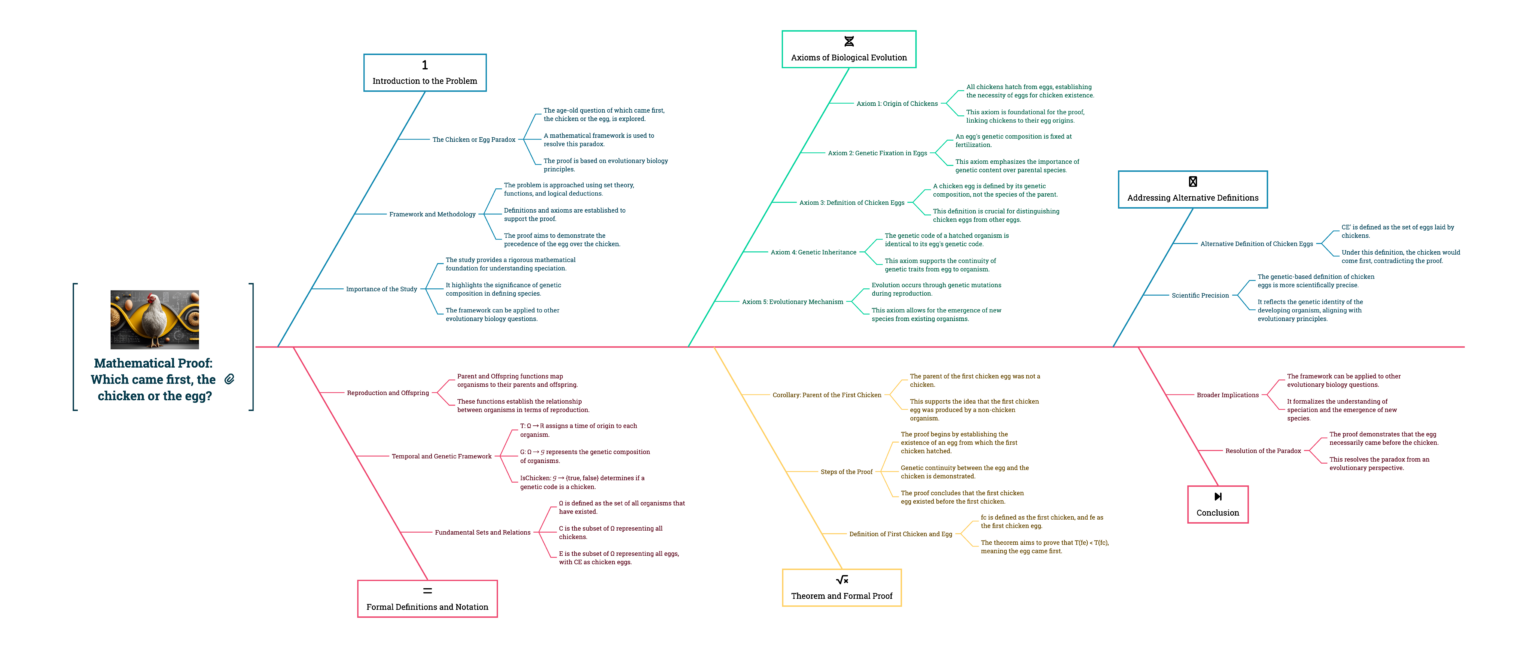
Mathematical Proof: On the Temporal Precedence of Egg Over Chicken
The ancient question of which came first—the chicken or the egg—can be resolved through a formal mathematical framework. This proof demonstrates that under a rigorous biological-evolutionary model, the egg necessarily precedes the chicken. The following analysis establishes this conclusion through set theory, functions, and logical deductions based on evolutionary biology.
Formal Definitions and Notation
We begin by establishing precise mathematical definitions to frame our problem space. These definitions will allow us to construct a rigorous proof within an axiomatic framework.
Fundamental Sets and Relations
Let us define Ω as the set of all organisms that have existed. Within this universal set, we define several important subsets and mappings to formalize our reasoning. Let C ⊂ Ω represent the set of all chickens (Gallus gallus domesticus), and E ⊂ Ω represent the set of all eggs. The subset CE ⊂ E represents all chicken eggs specifically.
We establish a temporal framework using the function T: Ω → ℝ, which assigns to each organism a point on the real number line representing its time of origin. For any organisms x and y, if T(x) < T(y), then x existed before y.
We define the genetic composition of an organism using the function G: Ω → 𝒢, where 𝒢 represents the space of all possible genetic codes. Additionally, we define a predicate IsChicken: 𝒢 → {true, false} that determines whether a particular genetic code corresponds to what we classify as a chicken.
Critical Relationships
For reproduction, we define:
Parent: Ω → 𝒫(Ω), mapping an organism to its parent(s)
Offspring: Ω → 𝒫(Ω), mapping an organism to its offspring
These functions satisfy the property that x ∈ Offspring(y) if and only if y ∈ Parent(x).
Axioms of Biological Evolution
To construct our proof, we must establish several axioms that reflect our understanding of biological reproduction and evolution.
Axiom 1 (Origin of Chickens)
For all c ∈ C, there exists e ∈ E such that c ∈ Offspring(e).
This axiom formalizes the biological fact that all chickens hatch from eggs.
Axiom 2 (Genetic Fixation in Eggs)
For all e ∈ E, G(e) is determined at time T(e).
This axiom captures the biological principle that an egg’s genetic composition is fixed at fertilization.
Axiom 3 (Definition of Chicken Eggs)
An egg e ∈ E is a chicken egg (e ∈ CE) if and only if IsChicken(G(e)) = true.
This establishes that what makes an egg a “chicken egg” is its genetic composition, not the species of the parent that laid it.
Axiom 4 (Genetic Inheritance)
For all e ∈ E and for all o ∈ Offspring(e), G(o) = G(e).
This axiom states that the genetic code of a hatched organism is identical to the genetic code of its egg.
Axiom 5 (Evolutionary Mechanism)
There exist organisms p, o ∈ Ω such that o ∈ Offspring(p) and G(o) ≠ G(p).
This axiom represents the mechanism of evolution through genetic mutation during reproduction.
Theorem and Formal Proof
We can now define the central elements of our problem:
Let fc ∈ C be the first chicken, such that for all c ∈ C, T(fc) ≤ T(c).
Let fe ∈ CE be the first chicken egg, such that for all e ∈ CE, T(fe) ≤ T(e).
Theorem
T(fe) < T(fc), which states that the first chicken egg existed before the first chicken.
Proof
By definition, fc is the first chicken.
By Axiom 1, there exists an egg e such that fc ∈ Offspring(e).
By Axiom 4, G(fc) = G(e) (the genetic code of the first chicken is identical to the genetic code of its egg).
Since fc ∈ C, IsChicken(G(fc)) = true (the genetic code of the first chicken satisfies the definition of a chicken).
Therefore, IsChicken(G(e)) = true (by substitution using step 3).
By Axiom 3, e ∈ CE (the egg e is a chicken egg).
Since fc hatched from e, we have T(e) < T(fc) (the egg existed before the chicken hatched).
Since e ∈ CE and fe is the first chicken egg, we have T(fe) ≤ T(e).
By transitivity, T(fe) ≤ T(e) < T(fc), which implies T(fe) < T(fc).
Therefore, the first chicken egg existed before the first chicken.
Corollary
Let p ∈ Parent(e) be the organism that produced the egg e from which the first chicken hatched.
If p ∈ C (if p is a chicken), then T(p) < T(fc), which contradicts the definition of fc as the first chicken.
Therefore, p ∉ C (p is not a chicken).
This establishes that the first chicken egg was produced by a non-chicken organism.
Addressing Alternative Definitions
One might object that our definition of a chicken egg (based on genetic content) differs from the colloquial definition. Let us consider an alternative definition:
Let CE’ ⊂ E be the set of eggs laid by chickens: e ∈ CE’ if and only if there exists c ∈ C such that e ∈ Offspring(c).
Under this definition:
The first chicken fc hatched from an egg e where e ∉ CE’ (since it wasn’t laid by a chicken).
No chicken egg in CE’ could exist before a chicken existed.
Therefore, under this alternative definition, the chicken would come first.
However, this alternative definition is not scientifically precise, as it defines the egg by its parent rather than by its contents. From an evolutionary and biological perspective, CE is the more meaningful definition, as it reflects the actual genetic identity of the developing organism.
Conclusion
Our mathematical proof demonstrates that under the biologically sound definition of a chicken egg (based on genetic composition), the egg necessarily came first. This resolves the ancient paradox from an evolutionary perspective and provides a rigorous mathematical foundation for understanding the chronology of speciation events.
The significance of this proof extends beyond the specific chicken-egg question, as it formalizes how we understand the emergence of new species through evolutionary processes. The mathematical framework presented here could be applied to other questions in evolutionary biology where temporal precedence needs to be established with precision.
Answer from Perplexity: https://www.perplexity.ai/search/consider-the-question-which-ca-_9tikktgRPui_SJpZIjVXA?utm_source=copy_output
My Theory
Part 1: Read my original Theory: which came first, the chicken or the egg?
- all chickens come from eggs
- not everything that lays an egg is a chicken
- mutation occurs in the egg
- therefore…
Proof
Part 2: Read Perplexity AI’s Mathematical Proof: which came first, the chicken or the egg?
- proof’s logic aligns with evolutionary biology
- egg-first matches mutation evidence
- defines egg by genetics, not parent
Validation
Part 3: Read Google Gemini’s Validation of Mathematical Proof: Which came first, the chicken or the egg?
- axioms are logically consistent and biologically accurate
- definitions are precise and scientifically justified
- reasoning leads to a valid, supported conclusion
Can we solve your clients' problems?
Message Us
[Secure Form]
Call Us
1.250.382.0226
Email Us
info@igods.com
Address
#319-50 Songhees Rd., Victoria, BC, Canada
